Vorweg ein kurzer, erstaunlicher Clip über Fibonacci und den Goldenen Schnitt
Die Fibonacci-Folge
Leonardo Fibonacci war ein italienischer Mathematiker (1175 - 1250). Er ist dafür bekannt, dass er im Westen die indisch-arabische Nummerierung anstelle der römischen Zahlen einführte. Im Jahr 1202 beschrieb er das Wachstum der Kaninchenpopulation in dem Werk Liber Abaci durch eine Folge ganzer Zahlen, in der jede Zahl die Summe der beiden Zahlen ist, die ihr vorausgehen. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... Diese Folge ist unendlich. Sie haben es verstanden: Um einen Term der Folge zu berechnen, müssen Sie einfach die beiden Terme vor dem Term addieren. Im obigen Beispiel ist die nächste Zahl 144 (55 + 89). Diese mathematische Folge hat zahlreiche Auswirkungen auf die verschiedensten Bereiche wie Botanik, Kunst oder Astronomie... Sie werden weiter unten sogar sehen, dass wir sie in den Regeln wiederfinden, die das Leben und das Universum bestimmen.
Die Fibonacci-Spirale
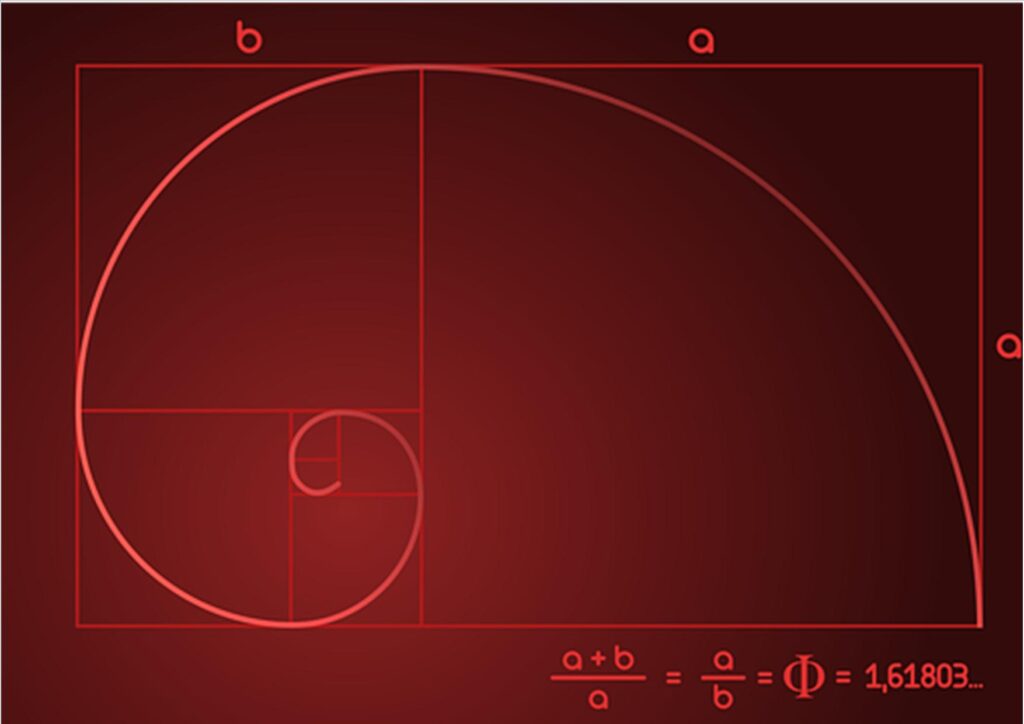
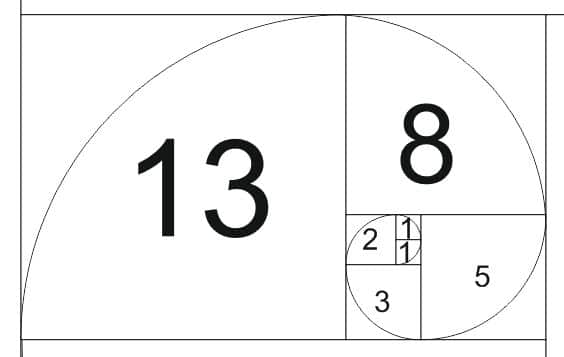
Es ist nicht einfach, die Fibonacci-Spirale mit Worten zu erklären. Sagen wir, wenn Sie Quadrate aneinanderlegen, deren Seitenmaße gleich den Zahlen der Fibonacci-Folge sind, erhalten Sie das nebenstehende Schema:
Wir können unendlich viele Quadrate aneinanderreihen, das Prinzip wäre genau dasselbe. Das nennt man eine fraktal : eine Struktur in der Struktur der Struktur...unendlich oft wiederholt. Unabhängig von der verwendeten Skala ist das Muster immer gleich! Das Video unten hilft Ihnen dabei, Fraktale (ein Begriff, der von dem Mathematiker Benoît Mandelbrot - aus dem Lateinischen fractus das bedeutet in Rechnung gestellt, gebrochen).

Sonnenblumenblüte, Fraktale, Fibonacci-Folge. So findet sich die Fibonacci-Spirale in Blumen, Bäumen, Tannenzapfen, Muscheln ...und :

Der Goldene Schnitt
Der Goldene Schnitt, der auch Phi genannt wird, ist = 1,61803. Diese sehr bekannte Zahl findet sich in sehr vielen Bereichen wieder: Architektur, Kunst...Für Mathematiker, die mehr über diese Zahl wissen möchten, die auch als göttliche Proportion lesen Sie den ausgezeichneten Wikipedia-Artikel zu diesem Thema. Interessieren wir uns stattdessen für Verhältnis zwischen der Fibonacci-Folge / -Spirale und dem Goldenen Schnitt. Es ist verblüffend.
Nimm beliebige Zahlen, die in der Fibonacci-Folge aufeinander folgen, und dividiere sie: Du erhältst den Goldenen Schnitt. Je höher die Anteile, desto höher die Genauigkeit. Wenn nämlich 3/2 gleich 1,5 ist, 610/377=1,61803.
Alles, was das Leben strukturiert, basiert auf diesen Proportionen: von der Spirale der DNA bis zur Spirale der Galaxie. Für manche ist das alles nur Zufall und Zufälligkeit, für andere ist diese Zahl geradezu mystisch. Ich bevorzuge die Vorstellung, dass die Natur nichts zufällig macht.
750 Millionen Iterationen (Wiederholungen) und immer noch die gleiche Struktur!
National Geographic: Video auf Deutsch, der Goldene Schnitt ist überall in der Natur zu finden
Der Amilo-Implosionsvortexer
Dieses geniale System wurde vollständig um die Fibonacci-Spirale und den Goldenen Schnitt herum entwickelt: Seine innere Struktur besteht aus Spiralen, die nach den Berechnungsprinzipien von Fibonacci und dem Goldenen Schnitt ineinander verschachtelt sind. Diese Spiralen verleihen dem Wasser eine Wirbelbewegung, die mit zwei Phasen verbunden ist: einer Expansionsphase, gefolgt von einer Schrumpfungsphase. Implosionswirbel (oder implosive Vortex). Diese Phasen sind auf die sehr durchdachte Gesamtform des Systems zurückzuführen. Die Implosionsvortexer verleiht dem Wasser zusätzliche Vitalität und eine wirbelnde Dynamik, die den ursprünglichen Quellen nahe kommt. Ihre Zellen werden so durch ein sehr hochwertiges, sogenanntes "lebendiges" Wasser tief mit Feuchtigkeit versorgt. Die Amilo-Filter für den Wohnbereich beinhalten den Implosionsvortexer serienmäßig.
Viele praktische Verwendungsmöglichkeiten
Bei Ihnen zu Hause, jeden Tag, findet der Amilo Vortexer seinen Platz in Ihrer Wohnung, um Ihnen "lebendiges" Wasser von hoher Qualität zu liefern. Entdecken Sie sie auf dieser Seite.